적도 근처서 나타났다 바로 사라지는 '쌍 소용돌이' 현상 54년 만에 수학모델로 증명

UNIST·서울대, 1971년 제시된 사도브스키 패치 입증…태풍연구 등에 도움 기대

적도 근처에서 드물게 관측되는 '쌍 소용돌이' 이론을 국내 연구진이 54년만에 수학적으로 증명했다.

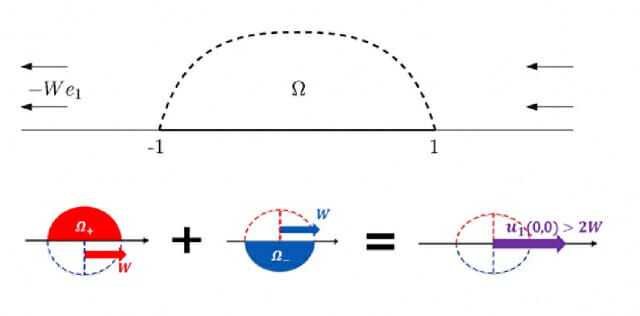
이 이론은 러시아 수학자 사도브스키(V. S. Sadovskii)가 1971년 서로 반대 방향으로 돌며 완전히 맞붙은 채로 움직이는 특수한 소용돌이 쌍을 수치 시물레이션을 통해 제시했다. 

사도브스키 패치로 알려진 이 모델은 당시 ▲바람이 완벽히 일정할 것 ▲마찰이 전혀 없을 것 ▲외부 방해가 없는 등의 이상적 유체 안에서 존재한다는 전제가 달렸다.

쌍소용돌이 난제를 54년만에 수학적 모델로 규명한 연구진. UNIST 최규동 교수(왼쪽)와 심영진 박사과정 연구생.

이 전제를 만족하면, 서로 반대 방향으로 돌며 회전 세기가 균등한 두 소용돌이가 맞붙은 상태에서 직진하게 된다. 

UNIST는 수학과 최규동 교수 연구팀(심영진 학생)과 서울대 정인지 교수 연구팀이 사도브스키 패치가 오일러 방정식의 해로서 존재할 수 있음을 수학적으로 증명했다고 2일 밝혔다.

오일러 방정식은 점성(마찰)이 없는 이상적인 유체가 어떻게 움직이는지를 설명하는 이론이다.

최규동 교수는 "수학적으로 존재를 증명하는 가장 확실한 방법은 사도브스키 패치의 모양과 운동을 동시에 설명하는 함수, 즉 유체의 운동법칙인 오일러 방정식의 해를 직접 찾아내는 것"이라며 "하지만 이러한 함수를 실제 구하는 것은 일반적으로 불가능에 가깝다"고 말했다.

두 소용돌이가 대칭축에서 완전히 접촉한 채 끊김 없이 이동해야 하는 특수한 구조 탓에 수학자들도 방정식 해의 ‘존재’를 논리적으로 입증하기가 쉽지 않다는 것이다.

연구팀은 그동안 이의 수학적 규명을 놓고, 북경대 황퉁 (Huang-Tong) 교수팀과 치열한 경쟁을 펼쳐 왔다.

최 교수는 "이번 성과는 단순한 사도브스키 패치의 수학적 존재성 뿐만 아니라 역학적 타당성, 즉 물리적 안정성도 함께 검증했다"고 강조했다.

연구팀은 이번 연구에서 변분법을 사용했다. 특정 조건을 만족하는 여러 가지 가능한 함수 중에서 주어진 값을 최대화 또는 최소화하는 함수를 찾는 방법이 변분법이다.

연구팀은 먼저 소용돌이 간격을 작게 설정하고 소용돌이 회전 세기에 상한을 두는 조건을 걸어둔 뒤, 그 안에서 운동에너지가 가장 큰 값을 갖는 소용돌이 쌍을 찾았다.

연구팀은 이렇게 얻어진 최대 에너지 소용돌이 쌍의 구조를 단계적으로 분석한 결과 그 모양이 사도브스키가 제안한 패치의 형태와 일치함을 확인했다.

연구팀은 이번 성과가 향후 난류 연구, 항공기와 선박의 후류 해석, 후지와라 효과와 같은 대기·해양 소용돌이 간의 상호작용 분야에서 유체역학적 이해의 토대를 넓혔다는 의미가 있다고 덧붙였다.

연구 결과는 수학 분야 국제 학술지 편미분방정식연보(Annals of PDE) 12월 호에 실렸다.

그림 위는 사도브스키 타입 소용돌이를 연구하는 전통적 접근 방식이다. 소용돌이 영역의 모양을 가정한 뒤, 그 경계가 오일러 방정식을 만족하도록 곡선 자체를 계산해 맞추는 방식이다. 그러나 이는 해(해당 소용돌이를 실제로 만들어내는 유동 함수)를 얻지 못하고, 단지 ‘그럴듯한 윤곽선’만 제시하는 데 그쳤다는 한계가 있었다. 아래 그림은 UNIST와 서울대 연구팀이 변분법으로 얻어진 최대화 함수가 사도브스키 타입임을 증명한 방법을 그림으로 나타냈다. (그림=UNIST)