'필즈상' 허준이 교수, '선 넘는' 연구로 수학 새 지평

조합론-대수기하학 접목...리드 추측, 로타 추측 등 수학계 난제 잇달아 해결

허준이 교수 (자료=IBS)

허준이 교수는 서울대에서 석사를 마친 후 해외 대학 12곳의 박사 과정에 지원했으나, 한곳만 빼고 모두 탈락했다.

그렇게 진학한 미국 일리노이주립대학 어바나샴페인 캠퍼스 박사 과정에 재학하며 허 교수는 수학계 난제 중 하나인 '리드 추측(Read's conjecture)'을 해결했다.

리드 추측은 영국의 수학자 로날드 리드가 1968년 제시한 문제다. 채색 다항식의 계수의 절대값이 갖는 성질에 대한 추측이다. 채색 다항식(chromatic polynomial)은 '그래프에서 인접하는 꼭지점에 서로 다른 색을 색칠하는 경우의 수'를 말한다.

미국 과학매체 퀀타는 허준이 교수와의 인터뷰 기사에서 이 문제를 이같이 설명했다.

간단한 그래프인 삼각형이 있다 하자. 이 꼭지점들에 색을 칠하는데, 같은 변에 맞닿은 꼭지점에는 같은 색을 칠할 수 없다. 꼭지점들에 색을 칠할 수 있는 방법은 몇 가지나 될까?

q개의 색깔이 있다면 처음에 칠할 수 있는 색은 q가지이고 다음에 칠할 수 있는 색은 (q-1)개, 그 다음에 칠할 수 있는 것은 (q-2)가지이다.

색을 칠할 수 있는 가지 수는 모두 합쳐 'q x (q – 1) x (q – 2) = q3 – 3q2 + 2q'이다.

(자료=퀀타매거진)

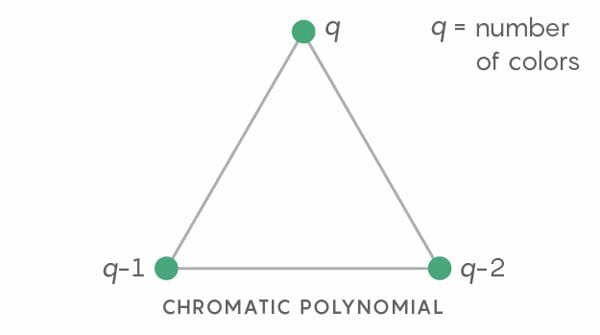
이 식에서 계수의 절대값은 순서대로 '1, 3, 2'이다. 이 숫자들은 늘어나다 가장 큰 수에 도달하고 이어 작아진다. 이처럼 채색다항식은 계수의 절대값이 정점에 이르기까지는 계속 늘어나기만 하고, 정점을 지나면 줄어들기만 하는 성질을 가진다고 리드는 추측했다.

또 그는 채색다항식에는 식을 이루는 양끝 계수의 곱이 가운데 있는 계수의 제곱보다 항상 작은 '로그-오목함(log concave)' 성질이 있다고 생각했다.

다각형에서 한 변을 없애면 칠할 수 있는 선택지가 커진다. 사각형에서 한 변을 없앨 경우 선택지는 삼각형의 꼭지점을 칠할 수 있는 가지 수만큼 늘어난다. 이때 로그-오목함의 성질은 복잡한 모습을 보인다.

(자료=퀀터매거진)

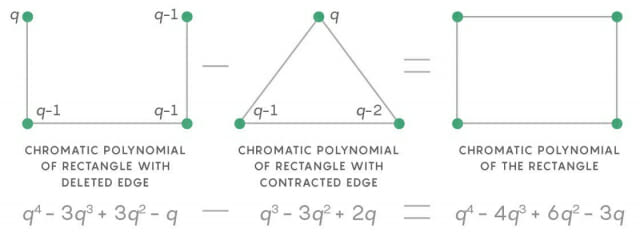
허 교수는 이 조합론 문제를 대수기하학을 적용해 풀었다. 그는 박사 과정에 진학하기 전 스승인 히로나카 헤이스케 서울대 석좌교수의 특이점 이론을 그래프에 적용하는 방법을 발견했다. 이 방법을 그래프에 적용하다 그래프가 로그-오목함을 보이는 이유를 설명할 수 있다는 것을 발견했다.

허 교수는 이에 흥미를 느껴 조사하다가 이 것이 '리드 추측'이라는 미해결 문제임을 알았다. 그는 문제를 알기도 전에 답을 갖고 있었던 것이다.

이 증명으로 학계의 주목을 받은 허 교수는 2011년 미시간대학 박사 과정으로 옮긴다. 여기서 그는 다시 리드 추측이 속한 더 큰 문제인 '로타 추측(Rota conjecture)'에 도전한다.

로타 추측은 리드 추측과 비슷하지만, 그래프 대신 '매트로이드(matroids)'라는 보다 추상적인 조합론의 연구 대상을 다룬다. 이탈리아의 수학자 로타는 1960년대 매트로이드에서 유추되는 다항식이 역시 로그-오목함 성질을 가진다고 예상했다.

허 교수는 에릭 카츠 오하이오주립대 교수와 카림 아디프라시토 에브류대학 교수와 함께 이 문제를 해결했다. 역시 조합론과는 무관해 보이는 '호지 이론'을 끌어와 적용했다. 호지 이론은 영국의 수학자 윌리엄 호지가 개척한 대수기하학 관련 연구다.

이후에도 그는 다변수 다항식의 한 종류인 '로렌츠 다항식'의 성질을 연구하는 등 지속적으로 주목할만한 결과를 내고 있다. 특히 조합론과 대수기하학 등 전혀 다른 분야의 직관을 접목하는 문제 접근 방식이 주목받는다.